The accuracy and speed of function approximations

The hard truth of function approximations is that they are not very accurate – that is why they are called approximations (duh). But just how accurate are the different approximations? Here I will take a look at the accuracy of the different sine function approximations.

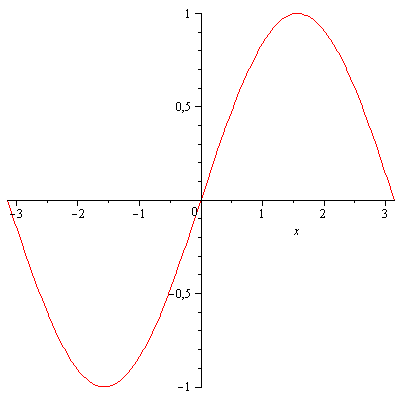
First off, what exactly are we going to approximate? Let us take a look at the sine function in a graph:

sine

The X axis goes from –π to π.

Let the approximation begin. We start out with a polynomial approximation. We simply use  a quadratic equation to approximate the curve of the sine function as best as we can. I came across a post where a guy used –π, -π/2, 0, π/2,π as points of reference and derived a function from that. He came up with:

image 

Without getting too much into the details, this quadratic equation only approximates the curve of the interval [0 ; π]. Putting this equation into a graph with the real sine function gives us this:

PolySine 
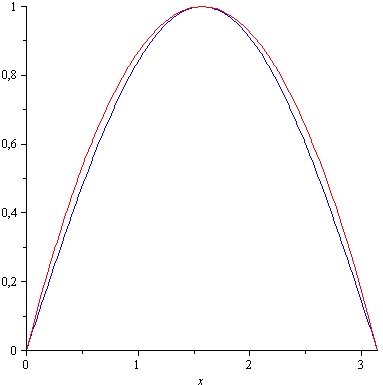
Blue is our sine function and red is our quadratic equation. As you can see, the quadratic function is exact in 0, π/2 and π. Now let us have a look at the good old Taylor Series approximation of sine:

TaylorSine 
Blue is our sine function and red is our Taylor series. Pretty neat huh? It is impossible to tell the difference between the two functions from the interval [0;π/2], but then it starts to deviate. Suffice to say that  that we can see from our results that the Taylor series approximation is more accurate – or is it? Stay tuned for part 2.

Update: part 2 is here

Comments

Post a Comment

Popular posts from this blog

.NET Compression Libraries Benchmark

Image
I often find myself needing a compression library in a software development project, and after a few tests with disappointing results I usually fall back to spawning 7Zip as an external process. This time however, the application specification prohibits any data written to disk, which 7Zip needs to do in order to work correctly. I needed to do everything in memory, and so I had to test some of the C# libraries available for compression as well as the different compression algorithms. Here is a full list of the tested libraries: .NET DeflateStream ICSharpCode SharpZip Zlib.NET DotNetZip Managed LZMA LZMA SDK QuickLZ    Compression 101 Before I get to the results of the benchmark, I think it is important to understand the different archive formats and compression algorithms in order to compare the results with other benchmarks/and or tests. Lets get to it! A compression algorithm can be compared to a small machine that takes in some data, do some math on it and...
Read more

Reducing the size of self-contained .NET Core applications

Just for note keeping, I've written down some methods of reducing the size of a .NET Core application. I thought others could use it as well, so here you go. Original Size First off, let's see how much disk space a self-contained 'hello world' application takes up. > dotnet new console > dotnet publish -r win-x86 -c release Size: 53.9 MB -  yuck! Trimming Microsoft has built a tool that finds unused assemblies and removes them from the distribution package. This is much needed since the 'netcoreapp2.0' profile is basically .NET Framework all over again, and it contains a truckload of assemblies our little 'hello world' application don't use. > dotnet new console > dotnet add package Microsoft.Packaging.Tools.Trimming -v 1.1.0-preview1-25818-01 > dotnet publish -r win-x86 -c release /p:TrimUnusedDependencies=true Size: 15.8 MB Much better! Although, we have only removed unused assemblies - what about unused...
Read more

Convex polygon based collision detection

Image
A lot of people have asked me: Why use a convex polygon only engine like Box2D? In this post I will provide some info on why convex polygons is the optimal polygon type to use. What does convex mean? Convex polygons needs to satisfy the following requirements: All internal angles must be below 180 degrees Every line segment between two vertices can be contained fully inside or at the edge the polygon A non-convex polygon is called a concave polygon and it must have an internal angle measuring greater than 180 degrees. As you might have thought about yourself; concave polygons can be quite handy. Convex-only engines can’t represent a simple player polygon like Pac-Man . Why use convex-only? There are really only one big juicy reason: performance Physics engines are able to take quite a few shortcuts and use cheap algorithms to determine the closest vertex, shortest distance and a lot more. An algorithm like Separating Axis Theorem and the Gilbert – Johnson –...
Read more